Page building status:
Page building status:Internal hyperlinks are being established, however they are not yet fully functional. Currently, they only work if the selected header is visible. I am searching for a way to get them to expand the containing headers and content of the selected header.
The PDF document will temporarily remain available until I am finished with the section on limits & derivatives, although using it for sections already covered here is not ideal (typos & errors).
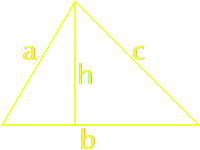
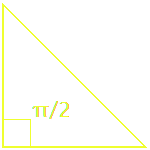
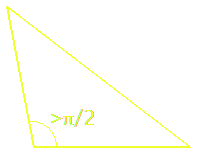
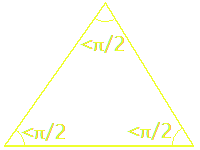


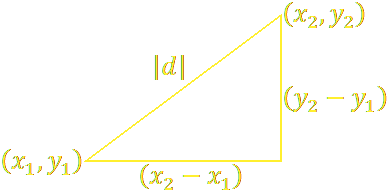
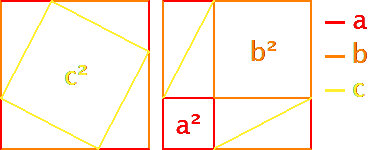 The square c² has area equal to all the triangle areas subtracted from the largest square,
$$c·c=(a+b)(a+b)-4·\Big(\frac{1}{2}·a·b\Big)$$
Expand,
$$c^2=a^2+2·a·b+b^2-2·a·b$$
Cancel like terms.
The square c² has area equal to all the triangle areas subtracted from the largest square,
$$c·c=(a+b)(a+b)-4·\Big(\frac{1}{2}·a·b\Big)$$
Expand,
$$c^2=a^2+2·a·b+b^2-2·a·b$$
Cancel like terms.